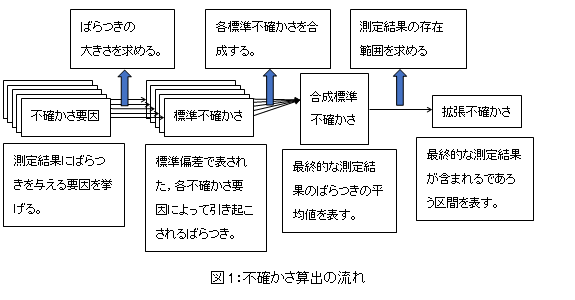
昨年、SUNATEC e－Magazine vol.139（2017年10月号）において、「不確かさ評価入門」と題して、測定の不確かさに関する必要性や、概要の解説を行ったが、今回はもう少し不確かさの算出法についての解説を行いたいと思う。ただ、「初級編」と銘打っているように、あまり複雑な内容については触れず、不確かさ評価の原理を知っていただくため、平易な内容にとどめている。また不確かさ評価と切っても切り離せないのが統計的手法である。本稿では不確かさ評価に必要な統計的手法についても解説する。

「不確かさ評価入門」にて不確かさについて簡単に解説したが、本項で不確かさの算出法の解説をする前に、簡単に振り返っておこう。

GUM¹⁾に規定された不確かさの定義は、
不確かさ・・・測定の結果に付随した、合理的に測定対象量に結び付けられ得る値のばらつきを特徴付けるパラメータ。
というものであった。つまり測定のばらつきを表すものが不確かさである。しかしその「ばらつき」は、通常のばらつきだけではなく知識の不完全さも含むということであった。

あと定義において重要なのは、不確かさは測定の結果、つまり値に付き、測定装置には付かない、ということであった。

次に不確かさを算出する手続きをおさらいする（図1）。不確かさ評価を行う際には、まず測定結果にばらつきを与える要因（これを「不確かさ要因」という）を挙げる。その後、その不確かさ要因によってどの程度ばらつくのかを実験等で求め、そのばらつきの大きさをいわば「ばらつきの平均値」である、標準偏差として表す。これを標準不確かさという。すべての不確かさ要因の標準不確かさを求めたら、それらを合成し、測定結果のばらつきである、合成標準不確かさを求める。合成標準不確かさもまた標準偏差である。つまり、測定結果が持つばらつきの平均値である。ただし、これまで測定結果の信頼性を表す方法としてよく用いられてきたのは、例えば、質量の測定結果であれば、

というような、値が含まれる区間を示す方法である。しかし、合成標準不確かさは標準偏差、つまりばらつきの平均値であるため、区間を表すものではない。よって合成標準不確かさを変形し、測定結果が含まれるであろう区間の半幅を表す値に変換する。その測定結果の存在範囲の半幅を表す不確かさを拡張不確かさという。

本稿では、上記で説明した不確かさの算出法の流れに従い、不確かさ評価法の原理と計算法の基礎を紹介する。

不確かさ評価を行う際には、まずどのような要因によって測定結果がばらつくのかということを決定する必要がある。不確かさ要因はもちろん測定の種類によって大きく異なるが、大まかなくくりで共通のものを示すと、「測定装置が原因の不確かさ」、「測定行為が原因の不確かさ」、「被測定物が原因の不確かさ」、「測定環境が原因の不確かさ」に分けられるだろう。

「測定装置が原因の不確かさ」で最も重要なのは、測定装置の校正の不確かさであろう。測定装置は上位標準によって校正されるが、完全な校正を行うことはできない。必ずそこには不確かさが存在する。さらにトレーサビリティ下位の測定装置では、上位標準の不確かさが校正のたびに受け継がれるため、下位に行くに従って不確かさは大きくなる。また測定装置が原因の不確かさでは、測定装置の長期安定性などがある。

「測定行為が原因の不確かさ」で必ず考慮されるのは測定の繰返し性（併行精度）である。また測定者によって測定結果が異なるような測定では測定者による不確かさもこれに含まれる。

「被測定物が原因の不確かさ」では、サンプリングによる不確かさなどはこれに含まれるだろう。また、被測定物の安定性なども含まれる。

「測定環境が原因の不確かさ」は室温や気圧、湿度によって測定結果が影響されるのであればこれらが不確かさ要因となる。

ただし、これらの不確かさ要因は完全に分類できるものではない。測定の繰返し性の中に被測定物が原因の不確かさも実は含まれているだろう。繰返し測定中に室温の変動がある場合には、繰返し性の中に室温変動の不確かさも含まれるだろう。このように不確かさの要因を決定するには今求めている不確かさ要因にどのようなばらつきが含まれているのかを考えて、ダブルカウントしないように配慮する必要がある。

また、不確かさ要因を決定する際に重要であるのは、小さな要因についてはあまり考慮する必要がない、ということである。最終的に各標準不確かさを合成して合成標準不確かさを求めるが、この不確かさを合成する手法は小さな要因が非常に影響しにくいものである。よって、小さな要因にこだわって細かな評価をしたとしても、結局合成を行ったときに全く効かなかった、いうこともよくある。上記のようなこと配慮して不確かさ要因を決定してほしい。

不確かさ要因が決定したら、それらの不確かさ要因によってどのくらい値がばらつくかを標準不確かさとして求める必要がある。GUMでは標準不確かさの求め方を2通り規定している。

一つはタイプAの評価法であり、もう一つはタイプBの評価法である。タイプAの評価法とは、実際に自分で測定を行い、複数のデータを得て、そのデータから標準偏差を算出する普通の方法である。タイプBの評価法とは、タイプAの評価法以外の方法を用いて標準偏差を求める手法である。例えば、文献値、論文等に載っている値を引用したりするのは自分でデータを得て評価したわけではないのでタイプB評価に含まれる。ここからは、タイプA、タイプB評価の詳細を見てみよう。

タイプA評価とは実際に自分で複数の測定データを得て、そこから標準偏差を求める手法である。タイプA評価で求められた標準偏差のことを「実験標準偏差」という。この実験標準偏差という用語だが、これは不確かさ評価でのみ用いられる用語であり、統計学では、「標本標準偏差」と呼ぶ。標準偏差とはいわば、ばらつきの平均値である。よってばらつきの平均値を出すためには測定データ一つ一つのばらつきの大きさを求め、その平均値を求めてやればよい。ではその算出法を考えよう。

表1で示す測定データを得たとしよう。

表1：測定データ

 

このとき、各データのばらつきの大きさを求めることを考える。各データのばらつきの大きさを求めるために必要なのが、「基準となる値」である。つまり、基準となる値から各データがどの程度離れているか、ということが各データのばらつきの大きさを表している。では基準となる値として適切なのはもちろん平均値（標本平均）である。では標本平均を求めてみよう。

次に各データと標本平均の差（残差）を求める（表2）。

表2：測定データと標本平均の差

 

これで各データのばらつきの大きさが求まった。ただし、この残差の平均を求めようとして、残差の和を取ると0となる。なぜなら残差には正のものも負のものも含まれるからである。ばらつきの大きさということは平均値からの距離が問題であり、正負は問題ではない。よって、すべてを正の値とするために残差を二乗する。さらに平均を求めるために、残差の二乗をしたものの和（二乗和）を求める（表3）。

表3：残差の二乗と二乗和

 

これで、ばらつきの平均を求めるための分子部分の和を求めることができた。あとは、データの個数で割れば平均だが、ここではデータの個数ではなく、（データの個数-1）の自由度と呼ばれるもので割らなければならない。なぜ自由度で割らなくてはならないのか、という詳細は他書²⁾に譲るが、簡単に説明すると、本当に意味のある残差の個数で割らなければ平均にならない、ということである。確かに表2で残差は5つ計算されているが、標本平均を用いて残差を計算しているため、すべての残差を足すと0になる、という縛りが存在する。つまり、5つの残差のうち1つが分からなくなったとしても、全残差の和が0となることを考えれば、他の4つの残差を足し合わせ、その値にマイナスを付ければ、分からなくなった残差を計算することができる。つまり、実質的に残差は5つではなく4つしか意味がないということになる。よって本当に意味のある残差の個数である自由度は、データの個数5から、残差を算出するために標本平均を1つ用いているということで、5-1=4となるのである。残差の二乗和を自由度で割った結果を式（3）に示す。

このs²(x)を実験分散という。先ほどと同じく、実験分散というのは不確かさ特有の用語である。統計では、標本分散という。この実験分散はもちろんばらつきを表すパラメータではあるが、単位が測定しているものとは二乗されているため異なっている。よって、測定データや、標本平均の値とばらつきの大きさを比較できない。次に単位を測定データと同じものに変換するために実験分散の正の平方根を求める。

このs(x)が実験標準偏差（標本標準偏差）である。通常標本標準偏差は「残差の二乗平均の平方根」と呼ばれるが、ばらつきの平均値といってもそう当たらずとも遠からずだ、ということが理解できるだろう。

さてここで、上記の測定を行った場合に測定結果を報告することを考えよう。上記の測定を行ったときの測定結果とは何だろうか？　通常標本平均である23.340 6 gを採用するだろう。では、その測定結果のばらつきの大きさはいくつだろうか？　実験標準偏差の0.248 2 gだろうか？　実はそうではない。なぜなら実験標準偏差は測定データが平均的にどのくらいばらついているのかを表している。しかし測定結果は標本平均である。よって標本平均のばらつきを求める必要がある。標本平均がばらつく、というのはイメージしにくいが、サイコロを考えてみよう。サイコロを5回振って標本平均を求めるということを繰返すと、異なる標本平均を複数得ることができるであろう。異なる標本平均を複数得ることができれば、その標本平均の実験標準偏差を求めることができる。ここで求めた標本平均の実験標準偏差は、測定データの標本標準偏差よりは小さな値になるだろう。なぜなら、例えばサイコロでは測定データを考えると、1や6の値が1/6の確率で現れる。しかし、5回の標本平均であれば、5回連続1や6が出ないと、標本平均が1や6になることはない。つまり、標本平均は測定データより中心に値が集まっているのである。よって、測定データの実験標準偏差が標本平均のばらつきであると考えるのは間違いである。標本平均の実験標準偏差を求めなければならない。

しかし、実際の測定において上記の手法のように標本平均の実験標準偏差を求めるのは難しい。なぜなら非常に多くの回数の測定を行わなければならないからである。通常上記のような手法は用いず、以下の関係式を用いて標本平均の実験標準偏差を求める。

つまり、測定データの実験標準偏差を繰返し回数の平方根で割れば、標本平均の実験標準偏差を求めることができるということである。確かに先ほど説明したように測定データの実験標準偏差より、標本平均の実験標準偏差のほうが小さくなるわけであるが、どのくらい小さくなるかというと繰返し回数の平方根で割った分だけ小さくなるということである。つまり、3回繰返しの標本平均より、10回繰返しの標本平均のほうがばらつきは小さくなる。これは当然であろう。それを数式で表したのが、式（5）であり、ここで求めた標本平均の実験標準偏差がタイプA評価によって求められた標準不確かさとなる。

実際に測定を行って実験標準偏差を求めるのがタイプA評価であるが、それ以外の手法によって標準偏差を推定するのがタイプB評価である。ここでは実際にどのような評価法を行うのかを紹介する。

まず、論文、データブック、校正証明書などから標準偏差や合成標準不確かさが分かっている場合はその値をそのまま標準不確かさと考えればよい。自分で取得した測定データから標準偏差を求めたわけではないので、タイプB評価と分類される。

次に標準偏差そのものが手に入らない場合には、その入力量がどのような確率分布に従っているのかということを、利用可能な情報から推定する。この確率分布というのは簡単にいうと、どのような形で値がばらついているのか、ということを表しているものである。

ではタイプB評価において用いられる確率分布で最も代表的な矩形分布について解説する。矩形分布とは、（ある値±a）の範囲内に値が存在する、というときに用いるものである。例えば、測定器の長期安定性に関する不確かさ評価を行いたいと考えた場合、その測定器は導入したばかりで自前では長期安定性を評価することができないとする。そのような場合メーカースペックに「長期安定性：±0.5 %」という記載があったとしよう。その場合図2に表す矩形分布（一様分布）を設定する。

上記のように矩形分布を設定した際の標準偏差は、分布の半幅を√3で割れば計算できる。この例では、

となる。つまり、タイプB評価で最も重要なテクニックは、何らかの情報から測定結果が含まれる範囲を見つけてくることである。その範囲が分かれば、矩形分布を設定¹し、分布の半幅を√3で割ることによって標準不確かさを求めることができる。

すべての標準不確かさを求めることができれば、標準不確かさの合成を行うが、ここで一つ考えなければいけないことがある。それは、標準不確かさの単位である。例えば、金属棒の長さ測定を行っている場合、測定の繰返しや、測定器の校正の不確かさはもちろん長さの単位で表されている。しかし、金属棒は温度によって長さが変化する。よって温度の不確かさを考えなければならないが、温度の不確かさの単位はもちろん℃である。そうすると不確かさを合成しようと思っても単位が異なるので合成できない。このような場合事前に単位をそろえる必要がある。この金属棒の場合であれば、線膨張係数と呼ばれる1 ℃温度が変化したときにどの程度長さが変動するかを割合で表したものがある。その線膨張係数の金属棒の長さを掛ければその金属棒が1 ℃温度が変化したときにどの程度伸び縮みするかがわかる。さらにそれに温度の不確かさを掛ければ、温度の不確かさ分温度がばらつけば、どの程度金属棒が伸び縮みするかがわかる。このように単位を変換するわけであるが、その単位を変換するための係数（金属棒の例の場合であれば、線膨張係数×金属棒の長さ）を感度係数という。単位を変換したい標準不確かさに感度係数を掛けることによって、出力量の単位に変換するということである。

これで標準不確かさを合成する準備が整った。標準不確かさを合成するには下に示す式（7）を用いる。

ここで、u1、 u2、 …は標準不確かさ、ucは合成標準不確かさである。この合成標準不確かさが測定結果のばらつきを表す標準偏差である。

合成標準不確かさはあくまでも標準偏差である。つまりばらつきの平均値である。ただし式（1）で示したように、測定結果の信頼性を表すときには値の存在範囲を示すことが一般によく用いられている。標準偏差は範囲を示す値ではないため、標準偏差から範囲を示す値を求める必要がある。安定している測定を行っている場合、測定結果は正規分布をしているとみなせる²。正規分布とは図3に示すきれいな山形の分布である。正規分布の重要な性質として、（平均値±標準偏差）の中に全データ中の約68 %が含まれ、（平均値±2×標準偏差）の中に全データ中の約95 %が含まれるというものがある。つまり、標準偏差である合成標準不確かさを2倍すれば約95 %が含まれる区間の半幅を表す値になるわけである。この約95 %含まれる区間の半幅を表す値のことを「拡張不確かさ」と呼び、合成標準不確かさを2倍したその2の値のことを「包含係数」と呼び、kで表す。つまり、合成標準不確かさを包含係数倍して拡張不確かさを求めるということである。それを数式で示したものが式（8）である。

ここで、Uは拡張不確かさである。拡張不確かさを報告するときには必ず包含係数も一緒に報告する義務がある。一般的な測定結果の報告法を下に示す。

このようにして最終的な測定結果が存在すると考えられる範囲を示すことによって、不確かさの報告を行う。逆に拡張不確かさとその包含係数が分かっていれば合成標準不確かさを求めなおすことができ、それをタイプB評価として採用することもできる。

さて、評価された拡張不確かさであるが、この例では有効数字2桁で報告している。ただし、不確かさは有効数字2桁目の数字に関してはほとんど信用することはできない。つまり、有効数字1桁目に関しては信頼性があるが（信頼性がある、というより、信頼性が保てるよう不確かさ評価を行う、といったほうが良いが。）2桁目については、例えば不確かさ評価をやり直すごとに値が変わることもあり得る。GUMでも不確かさを報告するときには多くとも2桁の有効数字で行うように、との記載がある。よって報告は有効数字1桁でも問題はない。測定結果はその報告する不確かさの有効数字に合わせなければならない。つまり、不確かさを評価すれば、測定結果がどの桁まで信用できるかが一目瞭然となる。たまに測定結果を測定器の読み値や平均値をそのまま多くの桁数で表記している例を見るが、不確かさ評価を行えば、どの桁まで表記すればよいか、という判断が簡単になる。

非常に簡単であるが不確かさ評価の流れと、その統計的手法の基礎を解説した。今回説明した内容は原理を解説しているのみであって、実際に不確かさ評価を行う際にはもっと考慮しなければならないことは多くある。本稿で興味を持たれた方は是非さらに不確かさについて調べていただきたい。それには、参考文献³⁾に挙げたURLを参考にしてほしい。これは筆者が所属するグループが運営しているWebsiteであり、不確かさに関する情報を多く提供しているので利用いただきたい。